Proporcionalidad II. Teoremas de la hipotenusa y Teorema del Cateto

MEDIA PROPORCIONAL

Dados dos segmentos a y b, la media proporcional es otro segmento x que cumple la proporción a/x=x/b.
También lo podemos expresar:

Podemos obtener la media proporcional de dos segmentos utilizando dos teoremas y la definición de potencia de un punto: 

1. Teorema de la altura 
2. Teorema del cateto
3. Potencia de un punto

1. Teorema de la altura

En todo triángulo rectángulo, la altura trazada sobre la hipotenusa es media proporcional entre los dos segmentos que determina sobre la hipotenusa.

c´/h=h/b´

Veamos su demostración matemática:

Aquí puedes ver una demostración gráfica con Geogebra

Trazado

EJERCICIOS DE APLICACIÓN:

1. Hallar el segmento x media proporcional, entre dos segmentos a , b dados.
2. Hallar dos segmentos x e y conocida su suma s y su media proporcional m
3. Hallar dos segmentos conocido su producto y su suma.
4. Trazar la raíz cuadradada de un segmento.

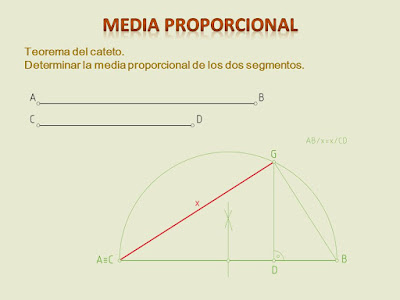
2. Teorema del cateto

En todo triángulo rectángulo, un cateto es media proporcional entre la hipotenusa y la proyección ortogonal de dicho cateto sobre ella.

Veamos su demostración matemática:

En este caso es aún más sencillo demostrar la semejanza entre triángulos, ya que ABC y ADC,comparten un lado y un ángulo, y son además rectángulos (es decir, otro de sus ángulos es de 90º) con lo que el tercer ángulo tendrá el mismo valor. Ambos triángulos tienen pues los lados proporcionales, es decir: AB/AC=AC/AD, es decir, AC equivale a la raíz cuadrada del producto AD y AB.

Puedes ver la demostración gráfica en la página dibufirst.

Trazado

3. Media proporcional por potencia de un punto con respecto a una circunferencia.

La potencia de un punto respecto a una circunferencia es igual al cuadrado de la tangente trazada desde el punto a la circunferencia.

Esta construcción se verá en un capítulo siguiente

• Demostraciones visuales con Geogebra de media proporcional en la web uno618.

EJERCICIOS DE APLICACIÓN

1. Hallar el segmento x media proporcional, entre dos segmentos a , b dados. (Realizar la construcción por ambos teoremas y por potencia)

2. Hallar gráficamente la raíz cuadrada de un segmento

4. Hallar el segmento x media proporcional, entre dos segmentos a , b dados.

5. Realiza el test de autoevaluación en Piziadas.

TEOREMA DE PITÁGORAS 

Fuente: Piziadas

Esta ecuación expresa que el área de un cuadrado de lado “a” es igual a la suma de las áreas de dos cuadrados, uno de lado “b” y otro de lado “c”. Si denominamos “a” a la hipotenusa (lado más largo) de un triángulo rectángulo y “b” y “c” a los catetos, gráficamente se puede representar con la siguiente figura.

Ver las diferentes demostraciones del teorema en Geogebra

REPRESENTAR NÚMEROS IRRACIONALES

Observa el triángulo rectángulo que construimos para representar raíz cuadrada de 2:

A partir de este triángulo podemos seguir construyendo para hallar raíz cuadrada de 3, de 4, 5, 6, etc.

La representación se puede realizar de dos modos:

Espiral de Teodorus

Representación gráfica de números irracionales en la recta numérica
Puedes descargar apuntes Cómo representar la raíz de 3 en la recta real 

REPRESENTAR PRODUCTO DE UN SEGMENTO POR UN NÚMERO IRRACIONAL 

Primero veamos:

Ahora veamos:

EJERCICIOS

1. Test de autoevaluación en Piziadas (Ir al final de la página)
2. Cuadernillo de ejercicios por Anabel Sanchez. Soluciones 1 y soluciones 2.
3. Geometría del triángulo rectágulo en Piziadas
4. Ejercicios de media proporcional.
5. Hallar gráficamente la raíz cuadrada de un segmento.

PROBLEMAS

1º BACHILLERATO

1. Hallar dos segmentos dadas sus suma y su diferencia.

2. Hallar dos segmentos conocida su suma y su media proporcional.

3. Hallar dos segmentos conociendo su suma y su producto .

 4. Dados dos puntos A y B, trazar por ellos dos rectas paralelas que disten una magnitud dada. (Fuente)

5. Determinar el segmento AB que pasa por P, conocido, cuyos extremos se sitúan sobre las rectas a y b respectivamente cumpliendose la relación PA=2PB.

6. Dado un punto exterior a un ángulo aOb, dibujar un segmento que tenga sus extremos en P y en b, de forma que la relación de distancias PM/PN=2/5.  (Ejercicio nº 2). Solución. Otra solución.

7. Dado un punto P interior a un ángulo aOb, trazar un segmento cuyos extremos estén en los lados del ángulo y quede dividido por P en dos partes iguales. (Ejercicio nº 1). solución.

8. Trazar por un punto P, una recta cuya razón de distancias a otros dos puntos M y N, sea Mr/Nr=3/2. (Ejercicio nº 3). solución.

2º BACHILLERATO

1. Hallar dos segmentos conocidos su diferencia y su producto.  (última página).

Otros problemas de operaciones con segmentos

1. Dados dos puntos A y B y una recta r que los separa, encontrar en ésta el punto P tal que la diferencia PA-PB sea máxima. Solución. 
2. Dados dos puntos A y B y una recta r tal que los dos puntos están en el mismo semiplano, encontrar en ésta el punto P tal que la suma PA+PB sea mínima. Solución.
3. Problemas con bolas de billar en uno618. Soluciones en Piziadas. 
1. Rebote a una banda. Explicación en Geogebra una banda (Extraído de Geometría dinámica)
2. Rebote a dos bandas.
3. Rebote a tres bandas. Reflexión y trayectoria

APUNTES

• Apuntes de Anabel Sanchez
• Demostraciones visuales con Geogebra en la web uno618.
• Extraídos de ÁREA DE DIBUJO. ES (Andalucía):
  • Operaciones con segmentos 2:
  • Segmentos irracionales: hallar la representación gráfica de raíz cuadrado de 2, 3, 4, 5, 6, 7, etc
  • Multiplicación de segmentos
  • División de segmentos
  • Halla dos segmentos conocidas su suma y su diferencia.

Entradas de Interés:

• wiki "Rincon de Artes y Dibujo"
• Introducción a la Geometría métrica y sus unidades didácticas. Web PIZIADAS.
• Geometría métrica y teorema de Pitágoras en la web PIZIDAS. Una visión muy interesante de todo lo que hemos visto en esta entrada desde un ángulo diferente, empezando con Pitágoras.
• En la misma página Teoremas de la altura y el cateto.
• Teorema de la altura y teorema del cateto Geogebra.