1. EQUIVALENCIAS. DEFINICIÓN
Decimos que dos superficies planas son equivalentes cuando tienen distinta forma e igual área.
Es decir, cuando nos presenten un problema de equivalencias lo primero que debemos hacer es igualar las diferentes áreas, lo que significa que debemos saber las fórmulas de las áreas de las diferentes figuras:
Es decir, cuando nos presenten un problema de equivalencias lo primero que debemos hacer es igualar las diferentes áreas, lo que significa que debemos saber las fórmulas de las áreas de las diferentes figuras:
2. RELACIONES BÁSICAS ENTRE FIGURAS
Para resolver problemas de equivalencia tenemos que conocer las siguientes relaciones entre figuras:- Triángulos equivalentes
- Triángulación. Convertir cualquier polígono en un triángulo equivalente.
- Equicomposición entre figuras.
- Triángulo y rectángulo equivalentes.
- Rombo y rectángulo.
- Rectángulo y trapecio isósceles
2.1 TRIÁNGULOS EQUIVALENTES. CONVERTIR CUALQUIER POLÍGONO EN UN TRIÁNGULO

Veamos:
Los tres triángulos tienen la misma base y la misma altura. Dado que el área de un triángulo equivale al producto de la base por la altura, podemos asegurar que en los tres casos la superficie es la misma.
EJERCICIO DE APLICACIÓN:
- Triángulo equivalente a otro, dado la base de dimensiones diferentes al dado. (fuente: La nube artística). Solución
- Triángulo isósceles equivalente a uno dado con diferente base.
- Rectángulo equivalente a otro con diferente base. (Solución)
2.2 TRIANGULACIÓN
De esta forma podemos eliminar uno o más lados de cualquier polígono, hasta convertirlo si así lo deseamos en un triángulo equivalente al polígono de partida.
EJERCICIO DE APLICACIÓN:
- Dado un triángulo dibujar el rectángulo equivalente.
- Dado un pentágono dibujar un triángulo equivalente.
2.3 EQUICOMPOSICIÓN
2.3.1 RECTÁNGULO EQUIVALENTE A CUALQUIER TRIÁNGULO
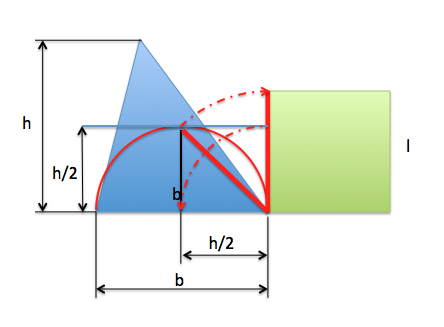
Un triángulo y un rectángulo con la mitad de la altura de un triángulo, tendrán siempre la misma, ya que el área de ambos será: b.a/2Las figuras están coloreadas así para que podamos apreciar su equicomposición, es decir, las formas de las que están compuestas ambas son las mismas.
2.3.2 ROMBO Y RECTÁNGULO
Un caso muy parecido el lo que pasa con el rombo y el rectángulo:
Fuente: la nube artística
2.3.3 TRAPECIO Y RECTÁNGULO
Y también sucede en el caso de un paralelogramo rectángulo A'B'C'D' equivalente a un trapecio escaleno dado ABCD, siendo su altura la misma que la de dicho cuadrilátero. Observa cómo los triángulos AA'M y MDD' son equivalentes, como también lo son los triángulos B'BN y NC'C.
EJERCICIO DE APLICACIÓN:
3. CUADRADO EQUIVALENTE A UN TRIÁNGULO
En general, para obtener una forma equivalente a otra dada, utilizaremos un cuadrado equivalente como forma intermedia entre dos figuras equivalentes. Por ello, analizaremos primero la forma de obtener un cuadrado equivalente a una figura geométrica. (Extraído de Piziadas).

Podremos utilizar cualquiera de las construcciones que utilizan formas cuadráticas, como las derivadas del concepto de potencia o los teoremas de la altura y el cateto que se obtienen a partir de la geometría del triángulo rectángulo.

Si utilizamos el teorema del cateto, la construcción será similar
Se incluye por último la construcción por potencia:
EJERCICIO DE APLICACIÓN:
- Dibujar el cuadrado equivalente a un cuadrilátero dado. (Construcción)
- Dado un cuadrado dibujar el rectángulo equivalente dado un lado. Solución en la pág. 3 de este pdf (Solución por tercera proporcional).
- Cuadrado equivalente a un rombo dado (Solución en la nube artística)
4. CUADRATURA DEL CÍRCULO
Se llama así al ejercicio de construir un cuadrado de igual área que el círculo dado. Si tenemos en cuenta lo siguiente:
El primer término del teorema Pi-r lo extraemos de la rectificación de una semicircunferencia:
Una vez conocido Pi-r, construyendo la media proporcional obtenemos el valor lado del cuadrado que buscamos:
Puedes visualizar todo el proceso con Geogebra aquí.
4.1 RECTIFICACIÓN DE LA CIRCUNFERENCIA (Repaso de 1º )
Se puede obtener la longitud de una circunferencia por diversos métodos, aunque su representación gráfica es siempre aproximada, dado que la función " PI" (3,1416...) es infinita y, por tanto, constituye una imposibilidad para poder operar con regla y compás.
- Método Specht
- Método de Arquímedes
- Método Kochansky Semicircunferencia.
- Rectificación de un cuadrante. Arco de 90º. Método Macheroni.
- Rectificación de una semicircunferencia por el método de los polígonos.
- Rectificar un arco menor de 90º.
- Rectificar un arco de más de 90º y menos de 180º. Y un ángulo mayor de 180º
5. CUADRADO DOBLE, EL TRIPLE, CUÁDRUPLE, ETC DE OTRO
El Teorema de Pitágoras (Ver en Piziadas), se aplica cuando la solución que buscamos es el doble, triple, cuadrúple, etc de un cuadrado dado:


EJERCICIOS:
- Dibujar el cuadrado que tenga el área doble, triple, cuádruple, etc de otro.
- Dibujar el cuadrado que tenga por área la suma de otros dos.
- Dibujar el cuadrado que tenga por área la suma de otros tres.
- Dados cuatro cuadrados, dibuja el cuadrado equivalente a su suma.


5.1 CIRCUNFERENCIA EL DOBLE, EL TRIPLE, CUÁDRUPLE, ETC DE OTRA
Este mismo conceptos se puede aplicar para el área de una circunferencia.
Gráficamente tenemos aquí el teorema de Pitágoras. De la misma forma los círculos inscritos en los cuadrados cumplen la misma condición que los cuadrados en el teorema: el área sumada de los dos círculos menores B C es igual al área del círculo mayor A.
EJERCICIOS:
- Círculo que tenga igual área que otros dos dados. Y círculo el doble, triple, cuádruple, etc de otro.
- Circunferencia equivalente a la suma de otras dos.
- Pentágono regular que tiene por área el doble de otro.
6. CÍRCULO EQUIVALENTE A UNA ELIPSE
En este caso, igualaremos las áreas de tal manera que obtendremos la expresión de la media proporcional: Radio circunferencia= semiejemenor x semieje mayor.
Construímos la media proporcional por cualquiera de los tres procedimientos explicados.
7. CUADRADO EQUIVALENTE A UN POLÓGONO REGULAR (Sin aplicar triangulación)
El área de cualquier polígono regular es:
Como la superficie de cualquier polígono regular se calcula multiplicando su apotema por el semiperímetro, la media proporcional de ambos segmentos será el lado del cuadrado equivalente.
En este caso se ha resulto por el teorema del cateto
APUNTES:
- Apuntes sobre equivalencias del IES FRancisco de Goya
- Descarga e imprime:
- Resumen de relaciones geométricas de la página laslaminas.es.
- Resumen sobre equivalencia de la misma página.
- Excelente presentación sobre equivalencia.
- Excelente explicación interactiva de todo el tema en "La nube artística".
EJERCICIOS
- Ejercicios para descargar e imprimir.
- 6 ejercicios de equivalencias
INFORMACIÓN DE INTERÉS:
- En Piziadas: Figuras equivalentes cuadrado equivalente.
- Equivalencias en Geogebra. Por Esther Alonso
- Ejercicios de equivalencias en Trapezoide.
- Una curiosidad: Historia de la cuadratura del círculo.


















No hay comentarios:
Publicar un comentario