Lo haremos a través de la presentación realizada por el profesor Juan Díaz Almagro, "Trazados fundamentales en el plano", la cual, debido a la extensa longitud, me he permitido la libertad de dividirla en diferentes bloques que os presentaré a continuación, también con la intención de adaptarla a mi discurso.
En la siguiente versión reducida recordaremos las siguientes construcciones que debes hacer para familiarizarte con ellas:
- Perpendicular a la recta por su extremo aplicando el teorema de Pitágoras.
- Paralelas a una recta a una distancia dada.
- Recta que pasa por un punto y sea concurrente con otras dos.
- Bisectriz de un ángulo cuyos lados se cortan fuera del dibujo
- Bisectriz de un ángulo mixtilíneo.
- Bisectriz de un un arco curvilíneo.
- Trazados de ángulos con el compás.
LUGAR GEOMÉTRICO
Para terminar, refrescamos el concepto de lugar geométrico a través del blog uno618, recordando algo muy sencillo, la mediatriz y la bisectriz, pero que hay que tener muy claro y que usaremos constantemente.También desde la página de dibufirst nos proponen recordar los lugares geométricos más habituales con gráficos interactivos.
APUNTES
- Apuntes del IES Elisa y Luis Villamil para 2º de bachillerato. Autores: José Ramón Martínez Soto y Mª Luz Rodríguez Somoza:
- Elementos fundamentales
- Paralelelismo
- Perpendicularidad
- Ángulos
- Distancias
- y muchos más que te recomiendo que descargues e imprimas.
- Lugares geométricos notables de la ed. Alarcón
- Apuntes de construcciones básicas y lugares geométricos. Ed. Sandoval
EJERCICIOS:
- Dados dos puntos A y B, trazar el arco de menor radio que pase por A y B. Trazar otros dos arcos, que pasen por A y B, cuyos centros disten 20 mm y 40 mm respectivamente de AB.
- Dadas dos semirrectas r y s que se cortan, trazar una circunferencia de 20 mm de radio que determine cuerdas de 14 mm de longitud sobre ambas rectas.
- Dada una recta r y un segmento AB, entre ello forman un cierto ángulo, determinar el punto S del segmento dado que equidista de los puntos de la recta r desde los que se ve dicho segmento bajo un ángulo de 40º. Solución
- Ejercicios para descargar e imprimir .
- Si se construyen rectángulos iguales entre si con cada lado del triángulo equilátero ABC, como se observa en el croquis, al unir los otros vértices de cada rectángulo se obtienen hexágonos. Calcular gráficamente el lado menor de los rectángulos para que sea regular el hexágono. (Solución)
- Trazar el lugar geométrico de los centros de circunferencias de radio 15 mm. que formen 45º con la circunferencia c y la recta r.
- Dibujar los posibles segmentos iguales y paralelos al segmento s, de modo que sus extremos estén en las circunferencias de centros O1 y O2. Solución.
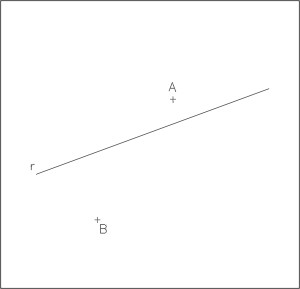
- Trazar dos rectas de forma que una de ellas pase por A y la otra por B, y que la dada r sea su bisectriz. (http://dibujotecnico.jmcastellanos.com/geometria/menu%20geometria.htm)
- 1. Determinación de un segmento conociendo su punto medio. Solución
- 2. Dada la recta r, la recta s y la circunferencia c, dibujar los posibles cuadrados que tengan una diagonal comprendida en r, un vértice en la circunferencia y otro en la recta s. Solución.
Observa la posible solución del problema para tratar de encontrar la resolución
- 3. ¿ Cuál sería la solución si en lugar de tener el vértice sobre l recta s lo tuviera sobre otra circunferencia dada ?.
- 4. Diferencia de cuadrados de distancias a dos puntos fijos.
- 5. Trazar el lugar geométrico de las circunferencias de radio 12 mm que forman 45º con una circunferencia en un caso, y con una recta en otro.
- 6. Ejercicio B1 junio 2002: Dadas las rectas paralelas r y s, trazar por un punto dado A, las rectas secantes en las que la parte comprendida entre las paralelas, sea igual a 30 mm. Solución
- Y un buen montón de problemas en Trazoide.
ENLACES DE INTERÉS
- Introducción histórica de la Geometría en "La espiral cromática". La geometría y los tensadores de cuerdas.
- En la espiral cromática: Geometría plana, métrica y euclidiana.







No hay comentarios:
Publicar un comentario