 |
| Para que conozcáis mejor a Escher |
Este tema lo vamos a dividir en tres capítulos:
El Dr. Néstor Martín Gulias, catedrático de dibujo técnico, arranca su blog sobre Tangencias por inversión de la siguiente manera:
"Una circunferencia se transforma en una recta según se incrementa su radio: una recta es una circunferencia de radio infinito".
Para calcular el inverso de un punto interno A se hace un segmento OA y se prolonga hasta que corte a la tangente por T, punto de intersección de la circunferencia y la perpendicular a OA por A.
A y A’ son inversos y siempre están alineados con O, que es el centro de inversión. Los puntos inversos de la circunferencia roja son dobles (inversos de sí mismos) por lo que se llama de autoinversión".
 |
| Fuente |
DEFINICIÓN
La Inversión es una transformación geométrica anamórfica ( la figura transformada es totalmente diferente a la figura de partida. Ver generalidades en este mismo blog). En la inversión se tienen que cumplir lo siguiente:- Dos puntos inversos (A, A’) están alineados con un punto fijo llamado Centro de Inversión (O).
- El producto de la distancia de un punto al Centro de Inversión por la distancia de su inverso al Centro de Inversión es constante (K) y se llama Potencia de Inversión.
 |
| K positiva |
 |
| K negativa |
Esto quiere decir que OA·OA’ = OB·OB’ = K
Si los puntos homólogos, A y A´, B y B´, ..., están a un mismo lado de O, la potencia es positiva.
Si están a distinto lado de O, K es negativa.
(Comprueba con la imagen interactiva del profesor Lúis Pérez si se cumplen estas propiedades)
PROPIEDADES DE LA INVERSIÓN
1. LOS PARES DE PUNTOS HOMÓLOGOS EN LA INVERSIÓN SON CONCÍCLICOS
Según la definición de potencia de un punto respecto a una circunferencia, se verifica que:
OA·OA’ = OB·OB’ = K,
Correspondiéndose con lo establecido para la inversión permite enunciar que dos pares de puntos homólogos en la inversión, son concíclicos, es decir, pertenecen a una circunferencia.
1.1 EJERCICIO:
Dados el centro de inversión, O y dos puntos homólogos A A´ y otro punto B, hallar su inversión.
1.2 EJERCICIO:
Dados dos puntos A A´, homólogos, en el centro de inversión O, y un punto B, en la recta que los contiene, hallar su homólogo.
Puesto que la potencia de inversión, K, implica que:
OA⋅OA´=OB⋅OB´=K
Si trazamos una circunferencia cualquiera AA´y una secante a ella que pase por O, se verificará:
OA⋅OA´=OM⋅OM
Determinando, Luego, la circunferencia que pasa por B M M, resultará en su intersección con la recta OA, el punto B´, homólogo de B.
OA⋅OA´=OM⋅OM
OM⋅OM=OB⋅OB´
OA⋅OA´=OB⋅OB´=K
OM⋅OM=OB⋅OB´
OA⋅OA´=OB⋅OB´=K
Cuando la potencia es negativa procederemos de la misma manera.
2. CIRCUNFERENCIA DE PUNTOS DOBLES
En la inversión de potencia positiva existen puntos dobles, es decir, homólogos de sí mismos.
Es evidente que:
Luego , la circunferencia de centro en O y radio
OT=K−−√ contiene a los puntos dobles. El segmento OT, por tanto es media proporcional OA y OA' y se resuelve utilizando la construcción del Teorema del Cateto.
Todos los puntos que pertenecen a ella tienen sus inversos en el mismo lugar. Coinciden por lo tanto A con A' y por extensión T con T'; esto significa que es una circunferencia doble (T = T') de puntos dobles.
Recibe el nombre de "circunferencia de autoinversión" o "circunferencia raiz de K".
2.1 EJERCICIO:
Dibuja el inverso del punto A (punto exterior), conociendo la c.p.d
Dibuja el inverso del punto A (punto interior), conociendo la c.p.d
2.2 EJERCICIO
Dibuja la circunferencia de puntos dobles dados el centro de inversión y una los puntos inversos A, A'.
 |
| Geogebra |
Este problema se resuelve por arco capaz del segmento OA' de 90º o mediante un tercer punto.
Veamos esta última solución:
Se elije un punto arbitrario B y calculamos el homólogo de B' por medio de una circunferencia auxiliar que pasa por A A' y B.
La potencia del centro de inversión O respecto a la circunferencia auxiliar es la potencia de inversión, dado que los puntos de tangencia desde O a dicha circunferencia han de ser sus propios inversos. Se traza la recta tangente desde O y el segmento OT es la raíz de la potencia y, por tanto, el radio de la circunferencia de puntos dobles buscada.
3. RECTAS INVERSAS DE SÍ MISMAS
4. CIRCUNFERENCIAS INVERSAS DE SÍ MISMAS
 |
| Geogebra |
Lo mismo sucede con todas las circunferencias que pasan por dos puntos homólogos. Sin ser dobles todos sus puntos (a excepción los de intersección con la circunferencia de puntos dobles, en la inversión de potencia positiva), son homólogas de sí mismas. Se cumple en todos los casos:
OA⋅OA´=OB⋅OB´=K
4.1 ÁNGULOS IGUALES QUE SE FORMAN
RECTAS ANTIPARALELAS
Dos rectas concurrentes en O son cortadas por dos antiparalelas respecto de ellas en puntos inversos de una inversión de centro O.
 |
| Ver gráfico de Esther Alonso |
Si se unen mediante rectas dos puntos AB y también sus homólogos A´B´, los ángulos en A´y B son iguales.
DEMOSTRACIÓN
El ángulo ABB´ y el AA´B´ son suplementarios porque ambos son ángulos inscritos y abarcan, entre los dos la circunferencia completa.
Siendo el ángulo OBA suplementario de ABB´, resulta que OBA = AA´B´
Aplicando el mismo criterio se demuestra la igualdad entre ángulos B´y A.
(Recomiendo que lo experimentes con Geogebra)
En la inversión de potencia negativa la igualdad de los ángulos de vértices en A´y B es inmediata, ya que ambos son inscritos que abarcan el mismo arco. Igualmente ocurre con los ángulos de los vértices A y en B´.
4.1.1 EJERCICIO
Determinar el inverso de un punto B dado el centro de inversión y el punto A y A'.
 |
| Geogebra |
Se traslada el ángulo en verde del punto B al punto A', en la intersección de A'B' con OB' se encuentra el punto buscado.
En inversión positiva se procede de la misma manera.
5. RECTA Y CIRCUNFERENCIA INVERSA
Por medio del siguiente gráfico interactivo podrás comprender visualmente que sucede con la inversa de una recta. Por Esther Alonso.
A continuación la lógica de la construcción:
De lo anterior resulta que, dada una inversión de potencia positiva, de las que se conoce su centro O y dos puntos homólogos A A´, si se traza una recta, r, por el punto A, perpendicular a la que los une con el centro de inversión, se puede determinar el homólogo de cualquier otro punto, B de r.
Para ello, se traza la recta que pasa por B O, sobre la que se encontrará B´en la intersección con la perpendicular a ella trazada por el otro punto, A´ homólogo del dado. (Ver en geogebra)
Atendiendo a los ángulos rectos construidos en B´(B) se comprueba que necesariamente se encuentran en sus vértices sobre la circunferencia que pasa por el centro de inversión y por el otro punto, A´(A), homólogo dado.
Si multiplicamos los miembros de la igualdad, tenemos que:
OA⋅OA′⋅OB⋅OB′=K2
Pero,
 |
| Geogebra |
De lo anterior resulta que, dada una inversión de potencia positiva, de las que se conoce su centro O y dos puntos homólogos A A´, si se traza una recta, r, por el punto A, perpendicular a la que los une con el centro de inversión, se puede determinar el homólogo de cualquier otro punto, B de r.
Para ello, se traza la recta que pasa por B O, sobre la que se encontrará B´en la intersección con la perpendicular a ella trazada por el otro punto, A´ homólogo del dado. (Ver en geogebra)
Atendiendo a los ángulos rectos construidos en B´(B) se comprueba que necesariamente se encuentran en sus vértices sobre la circunferencia que pasa por el centro de inversión y por el otro punto, A´(A), homólogo dado.
 |
| Geogebra |
Lo mismo pasa en una inversión negativa:
De todo ello, podemos decir:
La figura inversa de una recta (que no pase por O) es una circunferencia que pasa por el centro de inversión cuyo centro se encuentra en la recta perpendicular desde el centro de inversión a la recta original.
Recíprocamente la figura inversa de una circunferencia que pasa por el centro de inversión es una recta.
5.1 EJERCICIOS:
Realiza los dibujos con Geogebra y dibuja varios puntos homólogos de la recta y circunferencia para comprobar que es así.
- Se entregan los siguientes ejercicios para su realización y estudio: Inversión con soluciones del IES María Zambrano (ejercicio lámina nº 40). y Problemas de Inversión por Gonzalo Abella
 |
| Geogebra Interesante animación de este ejercicio. Por Esther Alonso |
6. CIRCUNFERENCIAS INVERSAS
Por medio del siguiente gráfico interactivo podrás comprender visualmente que sucede con la inversa de una circunferencia que no pasa por O. Por Esther Alonso.
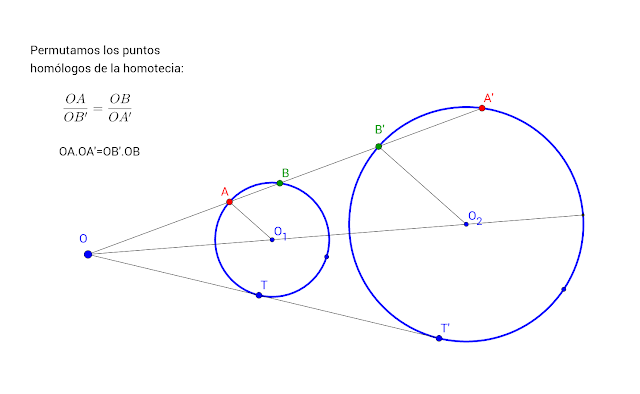
Dadas dos circunferencias O1 y O2, si se determina su centro de homotecia correspondiente, de razón positiva o negativa, y se permutan los puntos homólogos en la homotecia, se tiene: (Pincha para recordar que es la homotecia)
EXPLICACIÓN RAZONADA
Dadas dos circunferencias O1 y O2, si se determina su centro de homotecia correspondiente, de razón positiva o negativa, y se permutan los puntos homólogos en la homotecia, se tiene: (Pincha para recordar que es la homotecia)
Lo que demuestra que dos circunferencias (no tangentes ni concéntricas) son inversas con centros de inversión coincidentes con los de homotecia.
Si multiplicamos los miembros de la igualdad, tenemos que:
 |
| Geogebra |
Pero,
OA⋅OB=OT2
y
OA′⋅OB′=OT2
Sustituyendo
OT2⋅OT2=K
2
2
Es decir, que los puntos de tangencia de las tangentes comunes (exteriores o interiores) son homólogos en la inversión tanto positiva como negativa, que liga a las circunferencias.
Si una circunferencia tiene como centro el polo, su inversa será concéntrica a ella. Por tanto, para hallarla únicamente tendremos que trazar una circunferencia con centro en O y que pase por el inverso de un punto.
6.1 CASO PARTICULAR
 |
| Geogebra Esther Alonso |
Si una circunferencia tiene como centro el polo, su inversa será concéntrica a ella. Por tanto, para hallarla únicamente tendremos que trazar una circunferencia con centro en O y que pase por el inverso de un punto.
6.2 EJERCICIOS
Se entregan los siguientes ejercicios para su realización y estudio: Inversión con soluciones del IES María Zambrano (ejercicio lámina nº 41).
- Dados el centro de inversión, una circunferencia que no pasa por O y un par de puntos inversos A y A'. Determinar la inversa de la circunferencia. Este ejercicio se puede realizar por medio de tres procedimientos:
- Usando tres puntos.
- Usando tangente desde el centro de inversión.
- Usando dos parejas de puntos inversos.
- Dados el centro de inversión, una circunferencia que no pasa por O y la CPD. Determinar la inversa de la circunferencia. Este problema se puede resolver de dos formas:
- Usándo un diámetro alineado con el polo.
- Usando una recta tangente desde el polo.
- Inversión de una circunferencia exterior a la cpd. Por Esther Alonso
7. PROPIEDADES DE LA INVERSIÓN por medio de Geogebra
Comprueba las siguientes propiedades con Geogebra y la ayuda del profesor Jose Luís Taraba en los dos vídeos que dispone sobre este tema:
- 22 Geogebra y Matemáticas. Inversión respecto a una circunferencia I
- 23 Geogebra y Matemáticas. Inversión respecto a una circunferencia II
22 Geogebra y Matemáticas
En los siguientes vídeos vamos a comprobar visualmente muchas de las propiedades de la inversión:
- Al multiplicar las distancias al centro centro de dos puntos inversos se obtiene el radio al cuadrado.
- El centro de inversión y dos puntos inversos están alineados.
- Un punto y su inverso siempre están en distinto lado de la circunferencia.
- Si el punto está en la circunferencia, coincide con su inverso.
- El inverso del inverso es el punto de partida.
Además:
- Construye el inverso de un punto situado dentro de la circunferencia. Y lo mismo con un punto exterior.
- Dados dos puntos inversos respecto a una circunferencia, veremos como cualquier circunferencia que pase por los puntos es ortogonal a la circunferencia origen.
- Sean A, A´y B, B´dos puntos simétricos respecto a una circunferencia. Entonces los cuatro puntos están situados en una misma circunferencia. Son concíclicos.
23 Geogebra y Matemáticas
En este vídeo verás como comprobar las siguientes propiedades:
- Comprueba que la inversa de cualquier recta que no pase por el centro de inversión es una circunferencia que pasa por el centro de inversión. También el recíproco. Estudiar el caso de recta secante y recta tangente.
- La inversión transforma circunferencias en circunferencias.
- En la inversión se conservan los ángulos.
- Comprobar que las rectas que pasan por el centros y las circunferencias que pasan por dos puntos simétricos son objetos invariables.
APUNTES
- Ed. Alarcón
- Homología, Afinidad e inversión. Ed. Donostiarra
- Apuntes resumidos de Inversión del blog http://dibujotecnicoiyii.blogspot.com
- Apuntes y problemas del IES María Zambrano. Potencia e Inversión. Inversión con soluciones.
EJERCICIOS
- Descarga e imprime los problemas planteados en uno618
- 10 en dibujo. Examen de PAU en Madrid con problema de inversión.
- Indice de problemas de inversión en Trapezoide.
- Una buena colección de problemas de Inversión por Gonzalo Abella
ENLACES DE INTERÉS
CURIOSIDAD
- Cadena de Pappus
- Mecanismo de Peaucellier y Mecanismo de Hart
Veamos dos curiosos inventos que data de la Revolución Industrial que nos demuestra lo que acabamos de ver (fuente: uno618):









No hay comentarios:
Publicar un comentario